飲食店でのレジ閉め後に予想よりもお客様が少なく、冷蔵庫には材料が余ってしまった経験がないでしょうか?肉や野菜といった生鮮食品は保存できる日数も短く、廃棄しなければなりません。このような廃棄ロスをなくすには1日の注文数をできるだけ正確に予測することが必要になってきます。
レジスター専用機や手書きで1ヶ月分の売上や注文数を把握しようとすると手間がかかってしまいますが、POSレジシステムを使うと簡単に集計を閲覧、ダウンロードすることができます。今回は注文データの分析にあたって、飲食店向けPOSレジソフト「BeSHOKU」を使い、進めていきます。
まず、「BeSHOKU」の管理画面にアクセスし、「月間売上集計」を表示します。複数店舗を運営されている場合は「店舗名」、集計したい年月を「営業月」で指定し検索すると日次で合計売上金額や商品別の売上、注文数といったデータが表示されます。同画面の中に「CSV出力」ボタンがありますので、クリックしてダウンロードします。
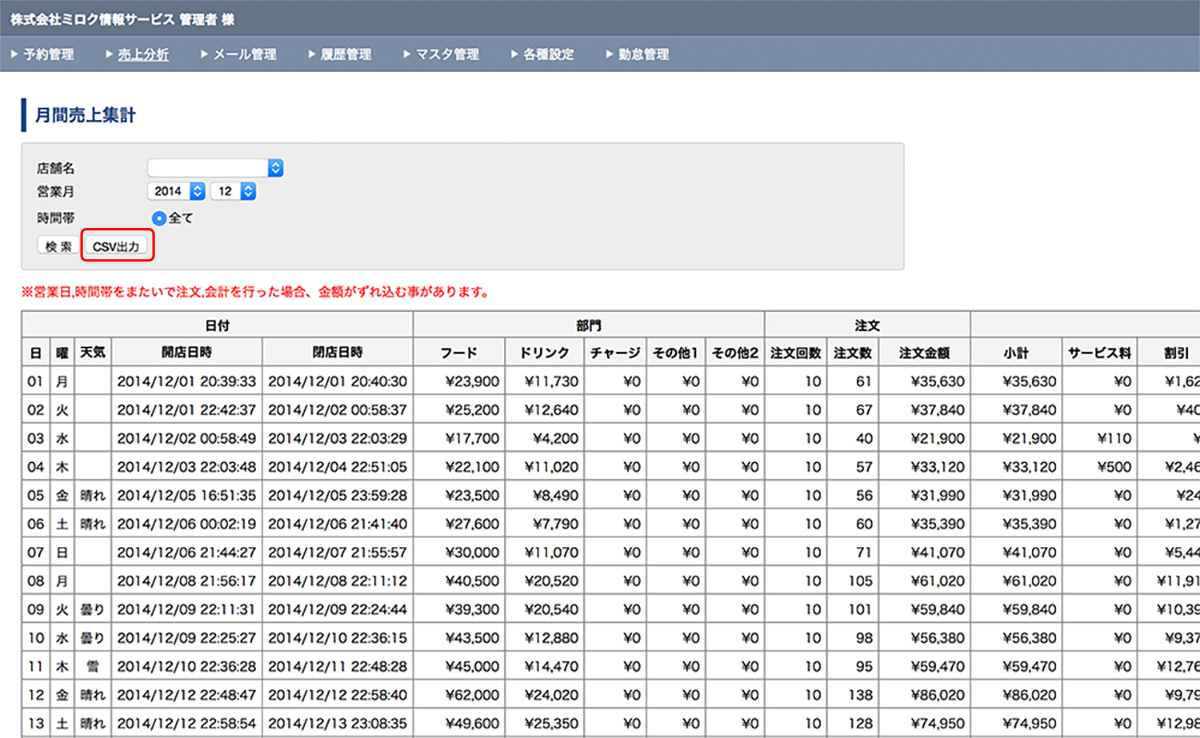
BeSHOKU月間売上集計画面
ダウンロードしたファイルをエクセルで開きます。この中の「日」「曜」「注文数」を抜き出します。
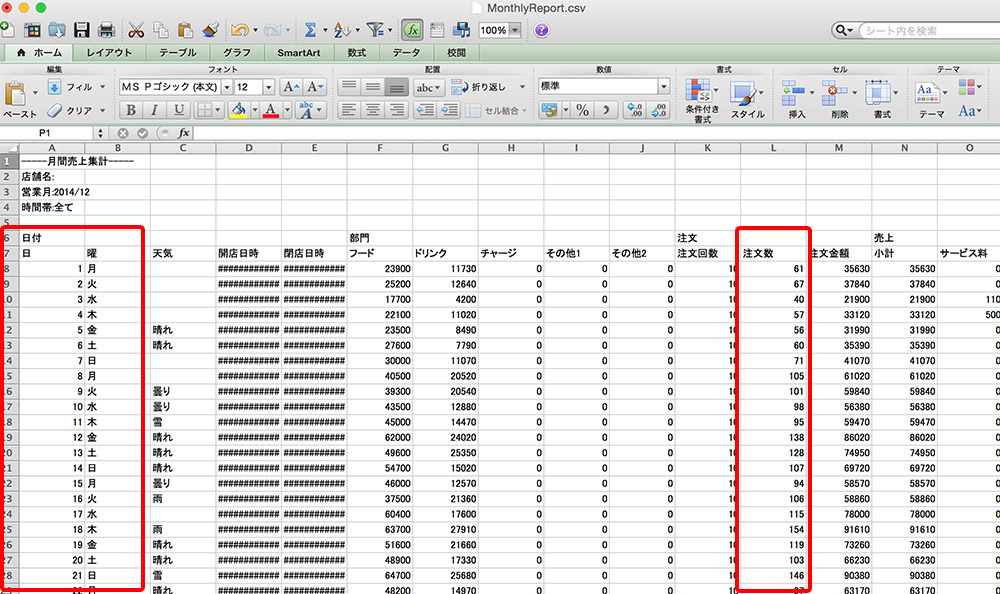
左から日付、曜日、注文数順に並び替えた後、一ヶ月分の注文合計数、平均、標準偏差、最小値、最大値、中央値を算出します。
エクセルの場合、関数を使うとそれぞれの値を一気に計算することが可能です。
合計の算出方法:C33のセルに合計を出したい場合、C33をクリックし、「=SUM(C2:C32)」と入力します。
平均の算出方法:C34のセルに合計を出したい場合、C34をクリックし、「=AVERAGE(C2:C32)」と入力します。
標準偏差(σ) の算出方法:C35のセルに合計を出したい場合、C35をクリックし、「=STDEV.P(C2:C32)」と入力します。
最小値の算出方法:C36のセルに合計を出したい場合、C36をクリックし、「=MIN(C2:C32)」と入力します。
最大値の算出方法:C37のセルに合計を出したい場合、C37をクリックし、「=MAX(C2:C32)」と入力します。
中央値の算出方法:C38のセルに合計を出したい場合、C38をクリックし、「=MEDIAN(C2:C32)」と入力します。
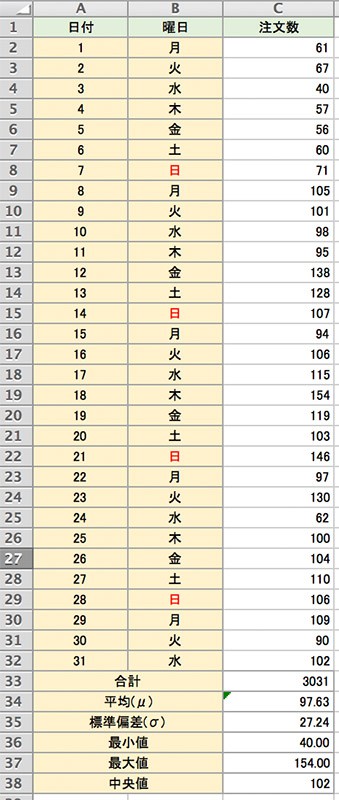
この中で出てきた「標準偏差」とは、データのバラつきを表す数値のことです。今回の飲食店の場合、1日の平均注文数が約98(四捨五入)、標準が27.24となっています。これは平均である98からマイナス約27の71からプラス約27の125までの範囲に68%の確率で注文がある、ということを示しています。標準偏差の値を2倍すると54になり、下は44から上は152までの中に95%の注文があることをし示します。つまり、標準偏差の数値が小さくなるほど、注文数のバラつきがすくなく、安定していると言うことができ、数値が大きくなるほど、日ごとの注文数の差が大きいと言えます。
また最後に「中央値」が出てきましたが、中央値は平均値と違い、データを大きい順に並べたときに真ん中に来る数値を表します。平均値の場合、飛び抜けて大きな数字や小さな数字があるとその影響を受けてしまいますが、中央値は影響を受けることがありません。この飲食店の例では平均値は97.63で中央値が102となっているのはそのためです。
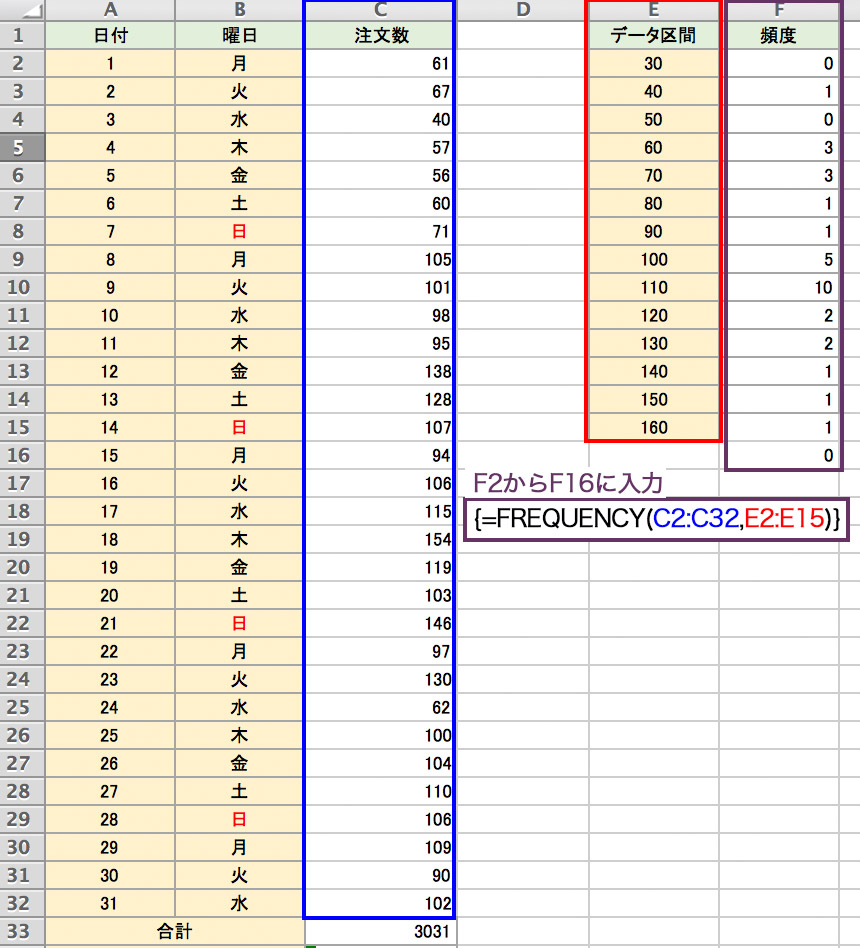
注文数を階級別にまとめ、ヒストグラム化すると中央値がわかりやすくなります。あるデータ区間に含まれるデータの個数を階級ごとに表示するには、エクセルのFREQUENCY(フレクエンシー)関数を使います。
まず、E列2行目から30、40、50…とまとめたいデータの区間を階級ごとに入力します。FREQUENCY 関数を使うことで30と入力した横のF列には21以上30以下に該当するデータの個数が自動的に入力されます。E列に30から160までの数字をセルに入力したら、F2からF15をクリックした状態で「=FREQUENCY(C2:C32,E2:E15)」と入力し、Control+Shift+Enterを同時に押します。すると、配列が自動で一括入力されます。なお、F16列目の0は自動的に入ります。
F列「頻度」の各数値にはそれぞれのデータ区間内にある注文数が入っています。これを見ると110が10と最も多く、中央値である102もこの階級に膨れ待ていることがわかります。
もっとわかりやすくするために、これを棒グラフにしてみます。
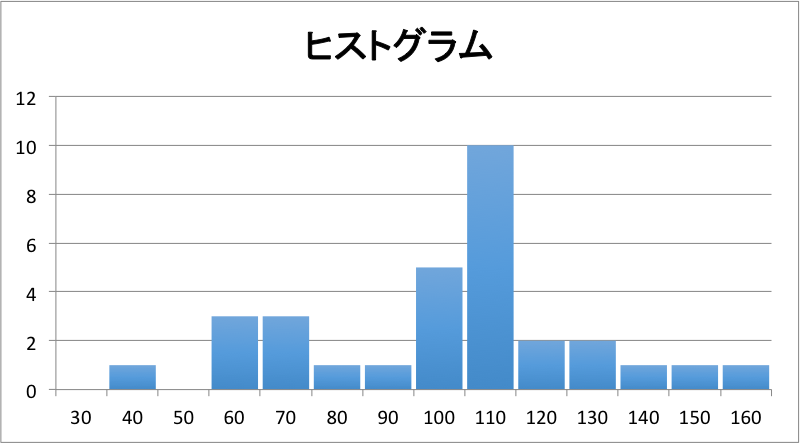
このグラフをヒストグラムといい、階級ごとのデータ個数、バラつきがわかるようになっています。1日あたり100〜110の注文があった日数が最も多そうですが、下は40から上は160まで日によって偏りがあることも見てとれます。では、一体どの程度の範囲で事前に注文数の目安を立てておけば良いのでしょうか?
正規分布とは中心が盛り上がった形をしたグラフのことをいいます。正規分布の中心は平均値になり、標準偏差との間には次のような関係があります。
グラフにすると次のようになります。
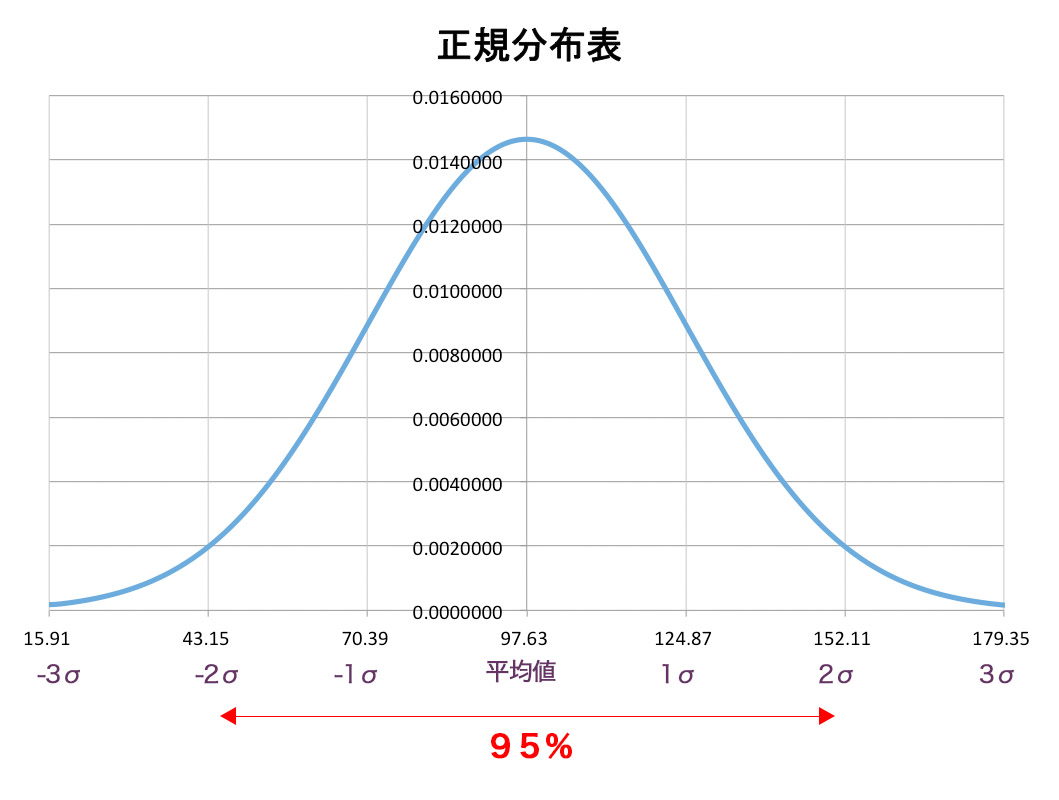
今回の飲食店の場合、平均が97.63で標準偏差は27.24なので、97.63±2×27.24=43.15〜152.11注文となり、かなりバラつきが多いことがわかります。そのため、毎日の仕入れ量を一定にしていると廃棄ロスが非常に多くなったり、逆に不足することが多くなったりすることがわかります。
この正規分布表は平均値と標準偏差がわかっていれば、Windowsのエクセルを使うとアドインの分析ツールから簡単に表示させることができます。macや主導で計算する場合はを使います。
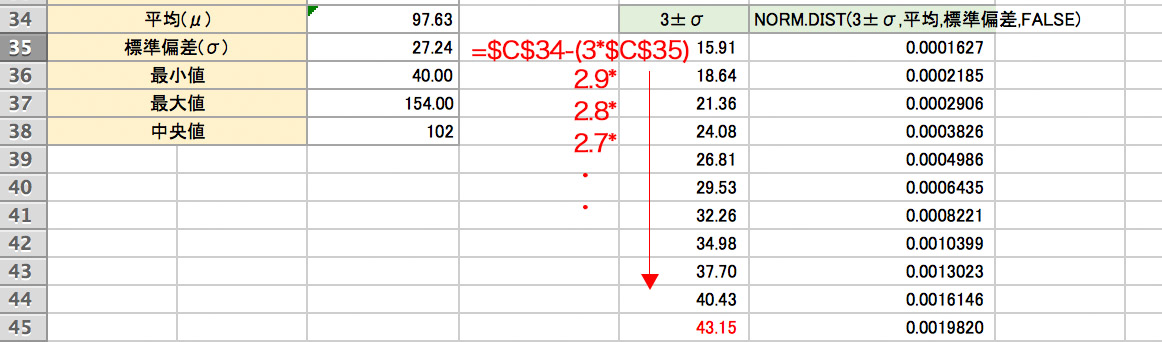
まず、セルに「=平均値-(3*標準偏差)」(上記例の場合、=$C$34-(3*$C$35))と入力します。次に下のセルに移動し、数字の3の部分を2.9にして再度計算、同じように2.8、2.7と数を0.1ずつ減らしていくと0.0で平均値と同じになります。今度は逆に「=平均値+(0.1*標準偏差)」として、0.1ずつ数を増やしていき、3.0になるまで繰り返します。今度は横の列に移動し、「=NORM.DIST(E35,$C$34,$C$35,FALSE)」と入力します($C$34は平均値、$C$35は標準偏差)。そのまま下セルに向かってドラッグすると計算式がコピーされます。全ての数値が出たら、グラフから「散布図(平滑線)」を選択すると、正規分布表が作成されます。
もし、このお店が1日に100の注文数を見越して仕入れをしているとした場合、どのくらいの確率で適正なのかを知るには「平準化」を行い、「標準正規分布表」と対応させることで知ることができます。
平準化 = (100 – 平均値) ÷ 標準偏差
平均値の97.63を四捨五入し98、標準偏差を約27とすると
(100 – 98) / 27 = 0.074074..
となります。
この数字を標準正規分布表に当てはめると0.5279に該当します。
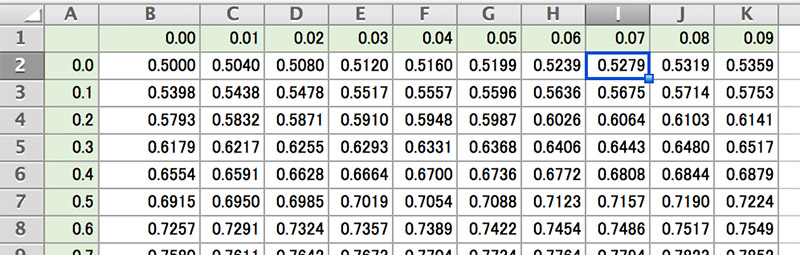
標準正規分布表は横軸に0.00〜0.09、縦軸に0.0から3.0までの数字を入れ、「=NORMDIST (B$1+$A2)」のようにして計算式を入力し作成します。
このことから注文数が100以下になる確率は52.79%となります。逆に100より多くなる場合が47.21%あることから毎日100の注文を見越した発注をしていた場合、余ることが多くなることが考えられます。
日によって来客数や注文数のバラつきが多いお店の場合、決まった量を毎日発注していると在庫過剰・不足によるロスが多くなることがわかりました。では、どのようにすれば適正な在庫数を予測できるのかを次に見ていきます。
1.累積確率で注文数見込みを付ける
平均値と標準偏差がわかると、何%の確率でどのくらいの注文数があるかを予測できるようになります。この計算にはエクセルの「NORMINV」関数を使います。まず、下側累積確率の数字を20%、40%、60%、80%と入力します。それぞれのセルの横列に「=NORMINV(20%,平均値,標準偏差)」「=NORMINV(40%,平均値,標準偏差)」・・と入力します。
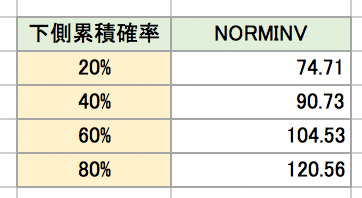
1日の注文数が74.71〜90.73になる確率が20〜40%、注文数が104.53〜120.56になる確率が60〜80%になる、ということがわかります。
2.曜日別に仕入れ量を決める
注文数には曜日や天候、イベントの影響によっても変動があると考えられます。オフィス街であれば平日に来客数は多く、土・日は少なくなったりするためです。そこで、曜日別に注文数を集計し、営業日数で割り、平均を算出。そこから標準偏差を出してみます。
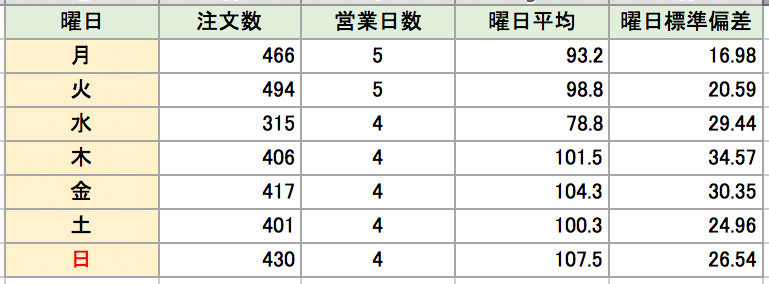
この表を見ると水曜が最も少なく、日曜が最も多くなっています。このお店では月〜水については仕入れ量を抑え、週末にかけて仕入れ量を多くするといった調整を行うことで無駄の少ない発注・在庫確保を行うことができるようになります。
面倒な計算式やグラフ化も一度テンプレートを作成しておけば、あとはPOSシステムの管理画面から月次の集計をダウンロードするだけで簡単に算出することができるようになります。
FreePOSに標準搭載された飲食店専用ソフトBeSHOKU、エステサロン・マッサージ、整体院向けソフトBeSALO、美容室・まつエク向けソフトBeEXTE、小売店向けソフトReTELAを使うと売り上げや顧客データをすぐに抽出することができるようになっています。
POSレジからのデータ集計を行うことのできる各ソフトの詳細やデモについてはお気軽にお問い合わせください。
